Mario Righi and Wolfgang J.R. Hoefer
A combination of Transmission Line Matrix (TLM) method and time domain mode matching is proposed. The resulting hybrid algorithm allows to take full advantage of the characteristics of time domain methods for regions with highly complex geometries while exploiting the efficiency of analytical formulations for the more regular regions. The approach is demonstrated for a packaged microstrip line containing a via-hole. While the planar circuit is discretized by a TLM mesh, the field in the package is decomposed into modal fields. The two sub-domains are joined by modal diakoptics. We thus obtain not only a significant reduction in computer time and memory, but also gain new insight into the physics of package resonance.
In time domain modal diakoptics the field is decomposed into a series of modes. The number of modes depends on the distance of the reference planes from the closest discontinuity, and on the spectrum of the excitation. All modal transmission lines are uncoupled and are terminated in the time domain by the convolution of the incident mode amplitude with its modal impulse response. The reflected mode amplitudes are then superimposed, sampled, and re-injected into the TLM mesh. The whole process can be described in compact form as follows:
![]()
where [V_i(k),V_r(k)] represent the incident and reflected voltage waves, [C] is the matrix that couples modes to TLM impulses, [J(k)] is a diagonal matrix containing the modal Green's functions, and * denotes numerical convolution.
By using the modal Green's function of a waveguide stub rather than the Green's function for a matched load it is possible to represent the upper part of the package in Figure 1. Note that the modal Short-circuit Boundary Conditions (SBCs) applied along the plane AA' have the following properties:
The packaged microstrip via-hole (Figure 1) has been discretized with a uniform TLM mesh of size delta_l=0.2 mm. A simulation has been performed for the full and for the segmented structure terminated with modal short-circuit boundary conditions. The SBCs have been placed at one third of the box depth, confining the standard TLM mesh to the complex region comprising the coax-to-microstrip transitions and the planar circuit. The TLM computational volume is therefore reduced by a factor three. This is confirmed by the comparison of mesh size and CPU time for the two TLM analyses is summarized in Table 1. Both memory and CPU time are reduced by 70% when diakoptics are used.
The S-parameters of the packaged microstrip line containing a via-hole obtained with the full and the reduced domain simulations using the above time domain waveforms are shown in Figure 2. The curves are overlapping. To further test the stability of the SBC, the number of modes included in the SBCs has been reduced to just the first three modes excited in the package (TM_y_01, TE_y_11 and TM_y_11). The corresponding S-parameters are shown in Figure 3. Note that the resonance due to the modes with order `21' has been lost. This resonance has been numerically suppressed by eliminating the corresponding Green's function.
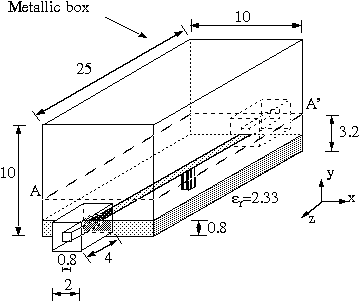
Figure 1: Geometry of a packaged microstrip via-hole (including coax-to-microstrip transitions). Strip width: 2 mm, via- hole size: 0.8 by 0.8 mm. All other dimensions in the figure are in mm.
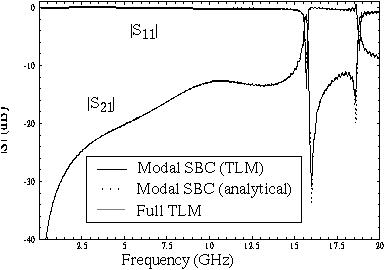
Figure 2: Magnitude of the S-parameters for the packaged microstrip via-hole (including coax-to-microstrip transitions).
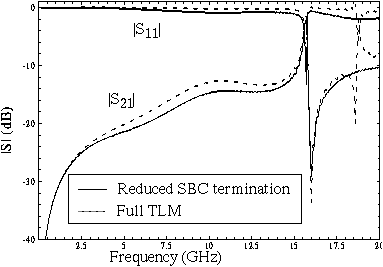
Figure 3: Magnitude of the S-parameters for the packaged microstrip via-hole (including coax-to-microstrip transitions). Modes up to the `11' order are included.
| Package | Mesh Size | CPU Time |
|---|---|---|
| Full TLM simulation | 50 by 50 by 165 | ~ 100 hr. |
| Segmented domain | 50 by 15 by 165 | ~ 30 hr. |
Table 1: Comparison of mesh size and CPU time for the analysis of the packaged microstrip via-hole. Simulation performed for 16000 time steps.
Further details can be found in:
M. Righi, W. J. R. Hoefer, "Efficient Hybrid TLM/Mode Matching Analysis of Packaged Components" to be presented at the 1996 MTT-S International Microwave Symposium, San Francisco, CA, June 1996.